Having just moved to a new city, you want to get to know your new surroundings. Your plan is to first explore the areas near your home, and then gradually expand the perimeter.

Basically, you are increasing the breadth of your familiarity with your new city gradually, starting from where you live.

When you conduct a search this way, you are using a search algorithm known as breadth-first search.

The Breadth-First Search (BFS) algorithm operates on graph data structures and is designed for searching through graphs. This tutorial will teach you how the BFS algorithm works. It will also give you an implementation of the algorithm in Typescript.

This tutorial is a follow-up to my previous article in which I explained graph data structures and also gave an implementation of graphs in Typescript. A knowledge of graphs is a necessary prerequisite to understanding the BFS algorithm. If you do not know graphs, please take some time to familiarize yourself here before moving forward.

What is Breadth-First Search?

The BFS algorithm is designed to traverse a graph starting from a single point. It visits the nodes closest to the start node, gradually increasing the distance from the start node. The algorithm ends when all of the graph's nodes have been visited or when a stop condition has been satisfied.

The BFS algorithm is a template for solving problems that involve searching a graph. BFS can be used to solve problems involving graphs, such as figuring out the shortest path between two nodes in a graph or figuring out if a path exists between two nodes in a graph.

REFLECTION

The BFS algorithm is a template for solving problems that involve searching a graph.

The BFS algorithm can be implemented both iteratively and recursively. Because recursion has an overhead cost and can be problematic when dealing with large graphs, the iterative implementation of BFS is preferred.

How the BFS algorithm works

The BFS algorithm works as follows:

• The start node and the graph to be traversed are passed as input parameters to the BFS function.
• We create a list to hold nodes that have been visited. When searching cyclic graphs, this prevents an infinite loop; it is not necessary when working with trees. A queue data structure is also declared to hold nodes that have not yet been visited. (Since queue data structures are not natively supported by Typescript, we can declare the queue as a list and use the shift method to remove from the head)
• We mark the start node as visited and push it into the queue.
• While the queue is not empty, we pop out the node (N) from the queue and if N’s neighbouring nodes have not yet been visited, we mark them as visited and then push them into the queue.

Now that we have a pseudocode for implementing the BFS algorithm, let's see an implementation of the algorithm in Typescript.

class Node<T> {
    data: T;
    adjNodes: Node<T>[];
    comparator: (a: T, b: T) => number;

    constructor(data: T, comparator: (a: T, b: T) => number) {
        this.data = data;
        this.adjNodes = new Array<Node<T>>();
        this.comparator = comparator;
    }
}

class Graph<T> {
    nodes: Map<T, Node<T>> = new Map<T, Node<T>>();
    comparator: (a: T, b: T) => number;
    root: Node<T>;

    constructor(comparator: (a: T, b: T) => number, data: T) {
        this.comparator = comparator;
        this.root = new Node<T>(data, comparator);
    }
}

/**
 * breadth-first search traversal of a node
 * @param {Graph<T>} graph - the Graph to be traversed
 * @param {Node<T>} startNode - the start node
 * @returns void
 */

export function bfs<T> (graph: Graph<T>, startNode: Node<T>){
    if (!startNode){
        return;
    }
    const visited: Node<T>[] = [];
    const queue: Node<T>[] = [];

    queue.push(startNode);

    while (queue.length !== 0){
        let current: Node<T>|undefined = queue.shift();
        if (!current){
            continue;
        }

        console.log(current.data);

        visited.push(current);
        current.adjNodes.forEach(node => {
            // if the node has not been visited
            if (visited.indexOf(node) === -1){
                visited.push(node);
                queue.push(node);
            }
        })
    }
}

Using a five-node graph, we will demonstrate the algorithm.

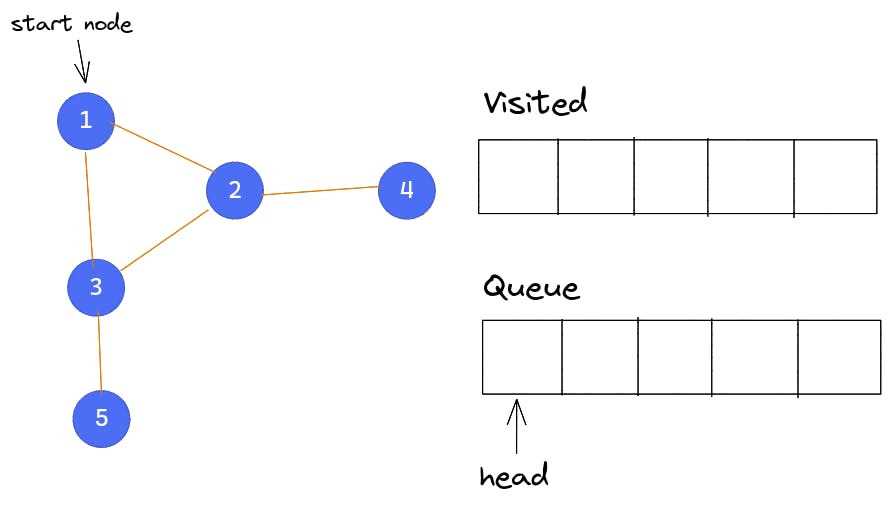
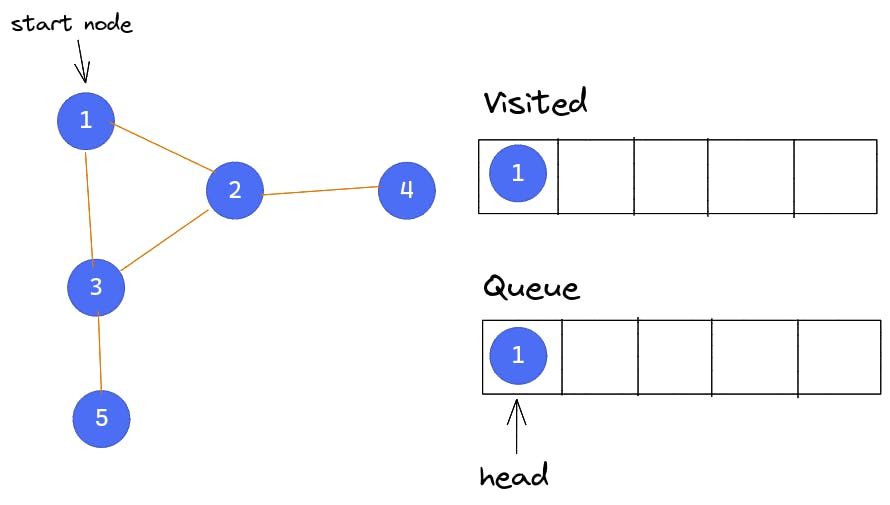
We begin with Node 1. BFS begins by marking Node 1 as visited and pushing it into the queue.

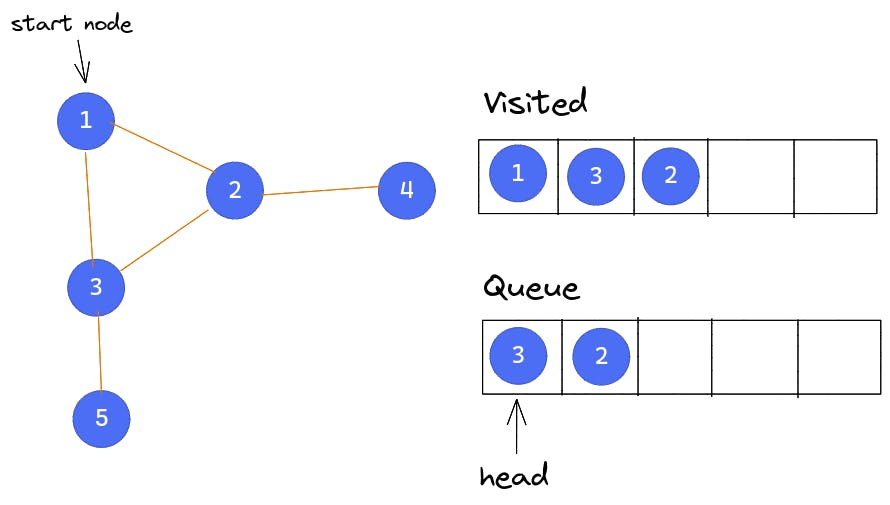
Next, Node 1 is popped from the queue and its two adjacent nodes (Node 3 and Node 2) are marked as visited and then all pushed into the queue as well. At this point, Node 3 is at the head of the queue.

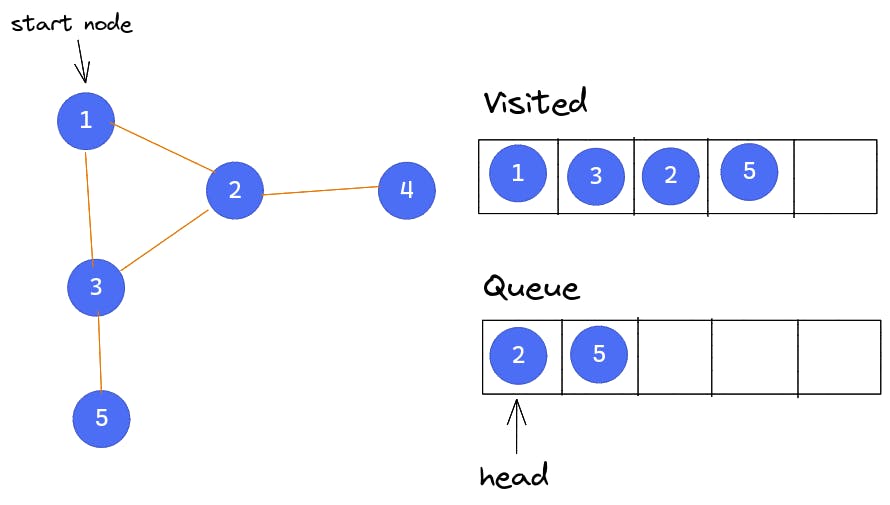
Node 3 is popped from the queue. As a result, Node 2 is now at the head of the queue. Node 3 is adjacent to Node 5 and Node 2. Node 5 is pushed into the queue, but since Node 2 has already been marked as visited, it is not pushed into the queue a second time.

Node 5 is a leaf node because it is not adjacent to any other nodes. Node 5 is popped from the queue and, since it is not adjacent to any other nodes, no node is pushed into the queue. This leaves Node 4 at the head of the queue.

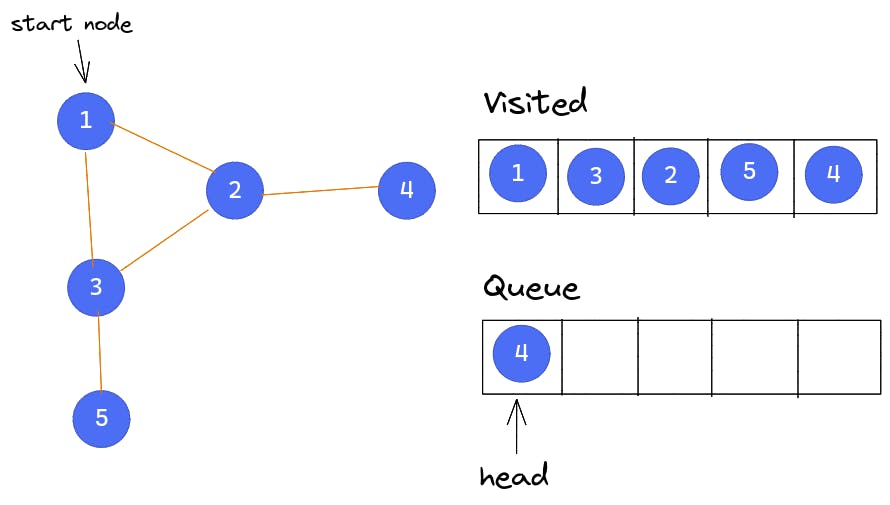
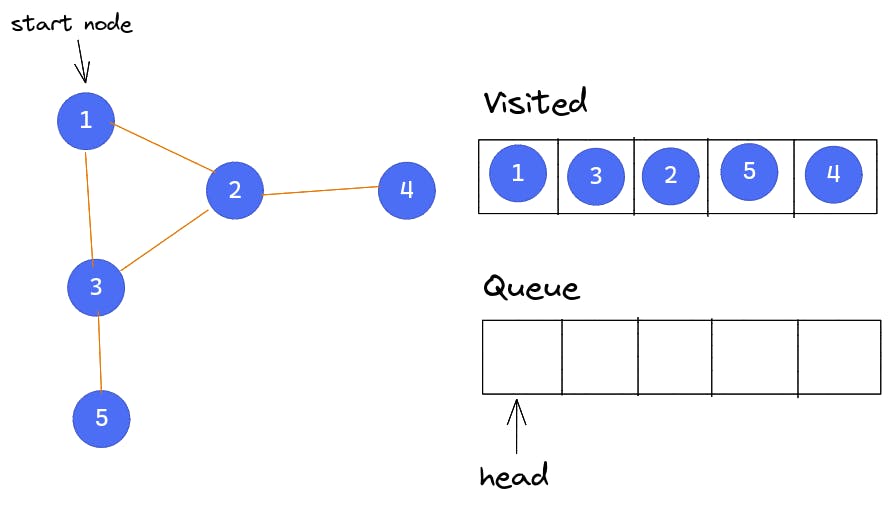
Node 4 is also a leaf node. It is popped from the queue and no other node is pushed into the queue. The queue is now empty, and as a result, the algorithm stops execution.

Time and space complexity of the BFS algorithm

When searching for an item in a graph, the worst-case scenario is that each node in the graph must be visited. Therefore, the time complexity of the BFS algorithm is dependent on the number of nodes in the graph. Also, for each node in the graph, the edges connected to that node must be explored. The worst-case scenario is that if we are dealing with a complete graph (where each node is adjacent to every other node), all the edges in the graph must be visited. This means that the number of edges in the graph also adds to the time complexity of the BFS algorithm. With all of these in place, the time complexity of the BFS algorithm is given as O(V+E), where V is the number of nodes and E is the number of edges in the graph.

The space complexity of the BFS algorithm, on the other hand, is given as O(V) where V is the number of nodes. This is because our queue and list of visited nodes can hold a maximum number of elements equal to the number of nodes in the graph.

Time complexity of the BFS algorithm: O(V+E)

Space complexity of the BFS algorithm: O(V)

Applications of the BFS algorithm

The BFS algorithm is a template for solving most problems that require searching a graph, so it is most likely that you will be adapting the algorithm to the problem that you are trying to solve. The BFS algorithm is very helpful for problems dealing with finding the shortest distance between two points. Other applications of the BFS algorithm include

1. GPS navigation
2. In Pathfinding algorithms
3. In Ford-Fulkerson algorithm to find maximum flow in a network.
4. Cycle detection in an undirected graph
5. In Minimum Spanning Trees

Conclusion:

I hope information shared this article was helpful to you. Now, its time to solve some BFS related questions. You can find some here on Hackerank and also here on Leetcode.

If you have any questions or suggestions, you can leave them in the comments section below, and I'll be happy to answer every single one.

If you like my content and would like to show some support you can buy me coffee